Assegnata la funzione
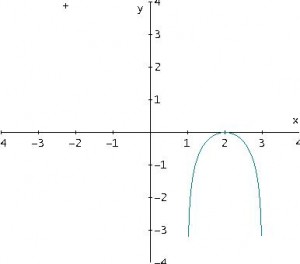
y = ln((x – 1)·(-x + 3))
il suo dominio in R è dato dai valori di x appartenenti a R tali che (x – 1)·(-x + 3) > 0
Risolvendo la disequazione prodotto SOLVE((x – 1)·(-x + 3) > 0, x)
si ottiene 1 < x < 3 che risulta essere il dominio della funzione.
Assegnata la funzione
y = ln(x – 1)+ ln(-x + 3)
che si ottiene dalla precedente applicando una delle proprietà dei logaritmi, il suo dominio in R
è dato dai valori di x appartenenti a R tali che x – 1 > 0 et -x + 3 > 0.
Si deve cioè risolvere un sistema di due disequazioni SOLVE([x – 1 > 0, -x + 3 > 0], [x])
si ottiene 1 < x < 3 che risulta essere il dominio della funzione.
In questo caso pur avendo risolto una disequazione prodotto e un sistema di disequazioni il dominio resta lo stesso; il grafico delle due funzioni sarà quindi lo stesso.
In altri casi il dominio cambia:
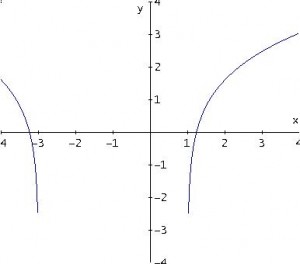
1 – y=ln((x – 1)·(x + 3))
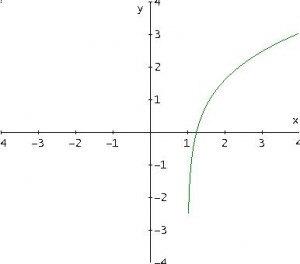
2 – y= ln(x – 1)+ ln(x + 3)
Grafico della 1
Dominio: x<-3 v x>1 (si risolve una disequazione prodotto)
Grafico della 2
Dominio: x>1 (si risolve un sistema di disequazioni)

spiegazione comprensibile…complimenti
grazie! mi dispiace che prima non si vedessero i grafici: lo spazio web dove erano ha cancellato spazi non più utilizzati.
mt