Studio semplice di una funzione omografica
a x + b
y = ———– , c≠o
c x + d
2 x – 1
y = ———–
-x + 3
– Dominio: {x ∈ ℝ / -x + 3 ≠ 0, x≠ 3}
– Intersezioni con assi:
con asse x
2 x – 1
y = ———– , y = 0 per x = 1/2 , y=0
-x + 3
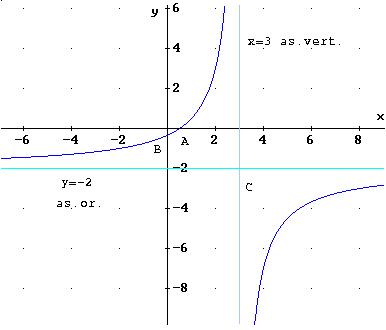
La funzione passa per il punto A (1/2,0)
con asse y
2 x – 1
y = ———– , x = 0
-x + 3
x = 0 , y = – 1/3
La funzione passa per il punto B (0, -1/3)
– Asintoti: x=-d/c x=3 asintoto verticale,
y=a/c y=-2 asintoto orizzontale
– Segno della funzione
2 x – 1
y = ———–
-x + 3
y > 0 N>0 x >1/2 ,
D>0 -x + 3 >0 -x>-3 x<3
N——————1/2++++++++++++++
D++++++++++++++++++++++3———
Si ha:
per x<1/2 y < 0
per x = 1/2 y = 0
per 1/2<x<3 y>0
per x=3 non esiste
per x>3 y<0
Si può poi fare una tabella per trovare le coordinate di qualche punto e tutte le informazioni vanno riportate nel piano cartesiano.
Se si studia la funzione con conoscenze superiori di Analisi Matematica, vanno calcolati limiti e derivata.
mtb

meno male ke state voi
e se il problema mi kiede di trovare la tangente in P (punto di intersezione tra l’iperbole e 1 dei due assi)?
metti a sistema l equazione dell’ iperbole con l’equazione di uno dei due assi
{[[y=0,],[equazione iperbole,]]
e poi fai la stessa cosa con x=0
Non capisco come faccio a disegnare quella parte dell’iperbole che non si interseca con gli assi…
Per Marta:
devi trovare le coordinate di qualche punto; per esempio, se ad x assegni il valore 4, per y ottieni -7. Hai quindi il punto (4,-7). Inoltre, una volta che hai disegnato un ramo, l’altro lo puoi ottenere per simmetria rispetto al punto di intersezione tra gli asintoti che in questo caso è il punto C(3,-2).
per Veronica e Andrea
un metodo è questo:
una volta trovato il punto di intersezione con un asse, per esempio con l’asse x, A(1/2,0), si scrive l’equazione del fascio di rette per quel punto che è:
y = mx – m/2.
Tale equazione si mette a sistema con l’equazione dell’iperbole e si ricava l’equazione di secondo grado in x risolvente il sistema. Poichè la retta deve essere tangente le soluzioni di tale equazione devono essere reali e coincidenti, e per questo motivo si impone che il delta sia uguale a zero.
Risolvendo si ottiene:
Delta=0
25m2-40m+16=0 che dà per soluzione m=4/5.
Si sostituisce m nell’equazione del fascio e si ha:
y=(4/5)x – 4/10.
Con lo studio delle derivate si può calcolare la derivata prima della funzione in x=1/2 ed ottenere m.
f'(x)= 5 /( (x – 3)2)
m= f'(1/2) = 4/5
Cosa succede al grafico della funzione se procediamo con il reciproco della funzione omografica di partenza? E come determinare dove una funzione omografica è crescente o decrescente?
per Paola
1) dove f(x)=0, la g(x)=1/f(x) non esiste, quindi l’asintoto verticale di g(x), per questo esempio sarà x=1/2
2) dove f(x) non esiste, g(x) ha un punto di intersezione con l’asse x. In questo caso g(x) passerà per (3,0)
3) il punto di intersezione con l’asse y che in f(x)è B(0, h) sarà, per g(x), (0,1/h)
4) L’asintoto orizzontale di f(x) è y=k (2/-1) e per g(x) sarà y=1/k (-1/2)
5) dove f(x) era crescente, la g(x) sarà decrescente (tenendo conto comunque dei domini f(x)e di g(x))
grazie mille!! meno male che l’ho trovata altrimenti mi sarei passato l’estate a studiare!!
maury, cosa significa di preciso?
mt
volevo sapere la definizione precisa della funzione omografica..
come si fa a vedere se è crescente o decrescente?
@katia: usando la derivata prima della funzione.
ad – bc
f'(x) = ———–
(cx + d)2
Quindi
se ad – bc>0 la funzione è crescente, se ad – bc<0 è decrescente.
trasformazioni geometriche che portano la funzione 1/X nella funzione omografica Y= (ax+b)/(cx+d)
e importante
trasformazioni geometriche che portano la funzione reciproco 1/x alla funzione omografica (ax+b)/(cx+d)
aiutatemi please